El Triángulo

Propiedades y tipos de triángulos:

Empecemos con las propiedades:

1. La suma de los ángulos interiores de un triángulos es igual a 180º.
2. Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
3. El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
4. En un triángulo a mayor lado se opone mayor ángulo.
5. Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales.
6. La suma de sus ángulos exteriores es 360º.

Clasificación hay dos tipos:

Según sus lados:

Triángulo equilátero: Tiene los tres lados iguales.

Triángulo isósceles: Dos lados iguales.

Triángulo escaleno: Tres lados desiguales.

Según sus ángulos:

Triángulo acutángulo: Tres ángulos agudos.

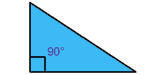
Triángulo rectángulo: Un ángulo recto. El lado mayor es la hipotenusa. Los lados menores son los catetos.

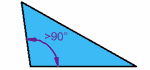
Triángulo obtusángulo: Un ángulo obtuso.

Rectas y puntos notables en el triángulo:

• Incentro: El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma (el radio de dicha circunferencia). Más concretamente, es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo (siendo una bisectriz la recta que divide a un ángulo en dos ángulos iguales).

• Baricentro: El baricentro (también llamado centroide) de un triángulo es el punto de intersección de las medianas de dicho triángulo (siendo una mediana el segmento que une un vértice con el punto medio del lado opuesto).

• Circuncentro: El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma (el radio de dicha circunferencia). En concreto, es el punto de intersección de las mediatrices del triángulo (siendo una mediatriz la recta perpendicular a un lado que pasa por el punto medio del mismo).

• Ortocentro: El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo (siendo una altura el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice).

Aquí os dejo un applet de GeoGebra, espero que así se os quede más claro la explicación anterior, por si queréis ver o utilizar cualquier APP os recomiendo GeoGebra, que además de manipular y realizar todo tipo de cosas con las matemáticas podréis ver representaciones de otros usuarios que son espectaculares y también os ayudará a comprender todo tipo de temas relacionados con las Matemáticas gráficamente : GeoGebra

El Teorema de Pitágoras:

Demostración gráfica:

Hacer lo de la pag manualmente

El teorema en 3D:

Teorema de Tales:

¿Cómo calcular la altura de un árbol a partir de su sombra?

Nosotros tenemos tres datos, la altura del palo(A'), la sombra del árbol(B) y la sombra del palo(B'). Lo que nos queda de incógnita es la altura del árbol. Lo que haremos a continuación se puede hacer de dos modos con una regla de tres o con una ecuación de primer grado. sería así: 

B/B'=A'/A(¿?)--> A¿?=B'*A'/B